PENDIENTE

Pendiente (matemáticas)

Ir a la navegación Ir a la búsqueda

Para otros usos de este término, véase Pendiente.

Pendiente de una carretera.

En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento lineal, natural o constructivo respecto de la horizontal.
En geometría analítica, puede referirse a la pendiente de la ecuación de una recta (o coeficiente angular)¹​ como caso particular de la tangente a una curva, en cuyo caso representa la derivada de la función en el punto considerado, y es un parámetro relevante, por ejemplo, en el trazado altimétrico de carreteras, vías férreas o canales.

Ángulo de inclinación

El ángulo α, definido tal como aparece en la figura, se llama ángulo de inclinación de la recta respecto al eje OX. La tangente (trigonométrica) del ángulo de inclinación ${\displaystyle \alpha }$ se llama coeficiente angular de la recta y se designa usualmente con la letra ${\displaystyle k}$ y entonces

${\displaystyle k=\tan(\alpha )}$

En realidad, el coeficiente angular y la pendiente tienen el mismo significado geométrico. En la ecuación ${\displaystyle y=kx+b}$ que involucra el coeficiente angular y la ordenada en el origen: k es el coeficiente angular y b la ordenada en el origen.²​

Pendiente de una recta

Pendiente: ${\displaystyle m={\frac {\Delta y}{\Delta x}}=\tan(\theta )}$

La pendiente de una recta en un sistema de representación rectangular (de un plano cartesiano), suele estar representada por la letra ${\displaystyle m}$, y está definida como la diferencia en el eje Y dividido por la diferencia en el eje X para dos puntos distintos en una recta. En la siguiente ecuación se describe:

${\displaystyle m={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}$

Geometría

Una recta horizontal tiene pendiente igual a 0 (cero). Cuanto menor sea el valor de la pendiente, menor inclinación tendrá la recta; por ejemplo, una recta que se eleve un ángulo de 45° con respecto al eje X tiene una pendiente ${\displaystyle m=+1}$, y una recta que caiga 30° tiene pendiente ${\displaystyle m=-0,5}$. La pendiente de una recta vertical no está definida, o se dice que es infinita.

El ángulo ${\displaystyle \theta }$ que una recta forma con el eje horizontal está relacionado con la pendiente ${\displaystyle m}$ por medio de la siguiente relación trigonométrica:

${\displaystyle m=\tan \,\theta }$

o equivalentemente:

${\displaystyle \theta =\arctan \,m}$

Dos o más rectas son paralelas si ambas poseen la misma pendiente, o si ambas son verticales y por ende no tienen pendiente definida; dos o más rectas son perpendiculares (forman un ángulo recto entre ellas) si el producto de sus pendientes es igual a -1.

La pendiente de las ecuaciones de la recta

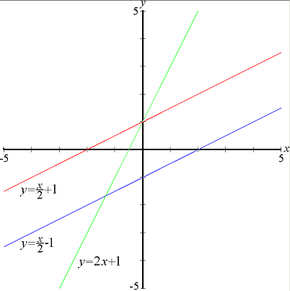
Tres líneas rectas — Las líneas roja y azul poseen la misma pendiente (m) que en este ejemplo es ½, mientras que las líneas roja y verde interceptan al eje y en el mismo punto, por lo que poseen idéntico valor de ordenada al origen (b) que en este ejemplo es el punto x=0, y=1.

Si y es una función lineal de x, entonces el coeficiente de x es la pendiente de la recta. Por lo tanto, si la ecuación está dada de las siguientes maneras:

${\displaystyle y=mx+b\,}$

entonces m es la pendiente. En esta ecuación, el valor de ${\displaystyle b}$ puede ser interpretado como el punto donde la recta se interseca con el eje Y, es decir, el valor de ${\displaystyle y}$ cuando ${\displaystyle x=0}$. Este valor también es llamado ordenada en el origen.

${\displaystyle y=m(x-a)\,}$

entonces "m" sigue siendo la pendiente. Pero en esta ecuación, el valor ${\displaystyle a}$ puede ser interpretado como el punto donde la recta se interseca con el eje X, es decir, el valor de ${\displaystyle x}$ cuando ${\displaystyle y=0}$. Este valor también es llamado abcisa en el origen.

Si la pendiente ${\displaystyle m}$ de una recta y el punto ${\displaystyle (x_{0},y_{0})}$ de la recta son conocidos, entonces la ecuación de la recta puede ser encontrada usando:

${\displaystyle y-y_{0}=m(x-x_{0})\,}$

La pendiente de la recta en la fórmula general:

${\displaystyle Ax+By+C=0\,}$

está dada por:

${\displaystyle m=-{\frac {A}{B}}}$

Propiedades

• Teniendo como datos los coeficientes angulares de dos rectas ${\displaystyle k_{1},k_{2}}$, uno de los ángulos μ formados por estas dos rectas se determina por la fórmula

${\displaystyle tan\mu ={\frac {k_{2}-k_{1}}{1+k_{1}k_{2}}}}$.

• La pauta de paralelismo de dos rectas es la igualdad de sus coeficientes angulares

${\displaystyle k_{1}=k_{2}}$.

• La pauta de perpendicularidad de dos rectas se determina por las relaciones:

${\displaystyle k_{1}k_{2}=-1}$ o ${\displaystyle k_{2}=-{\frac {1}{k_{1}}}}$.³​

• Si en la ecuación ${\displaystyle y=kx+b}$ se mantiene constante k, sólo varía b, se tiene una familia de rectas paralelas con coeficiente angular constante k, que cubre todo el plano, al recorrer b todo el conjunto ℝ.

Cálculo

El concepto de pendiente es central en el cálculo diferencial. La pendiente de una recta es la tangente del ángulo que forma la recta con la dirección positiva del eje de abscisas. En funciones no lineales, la razón de cambio varía a lo largo de la curva. La derivada de la función en un punto dado es la pendiente de la línea tangente en dicho punto.